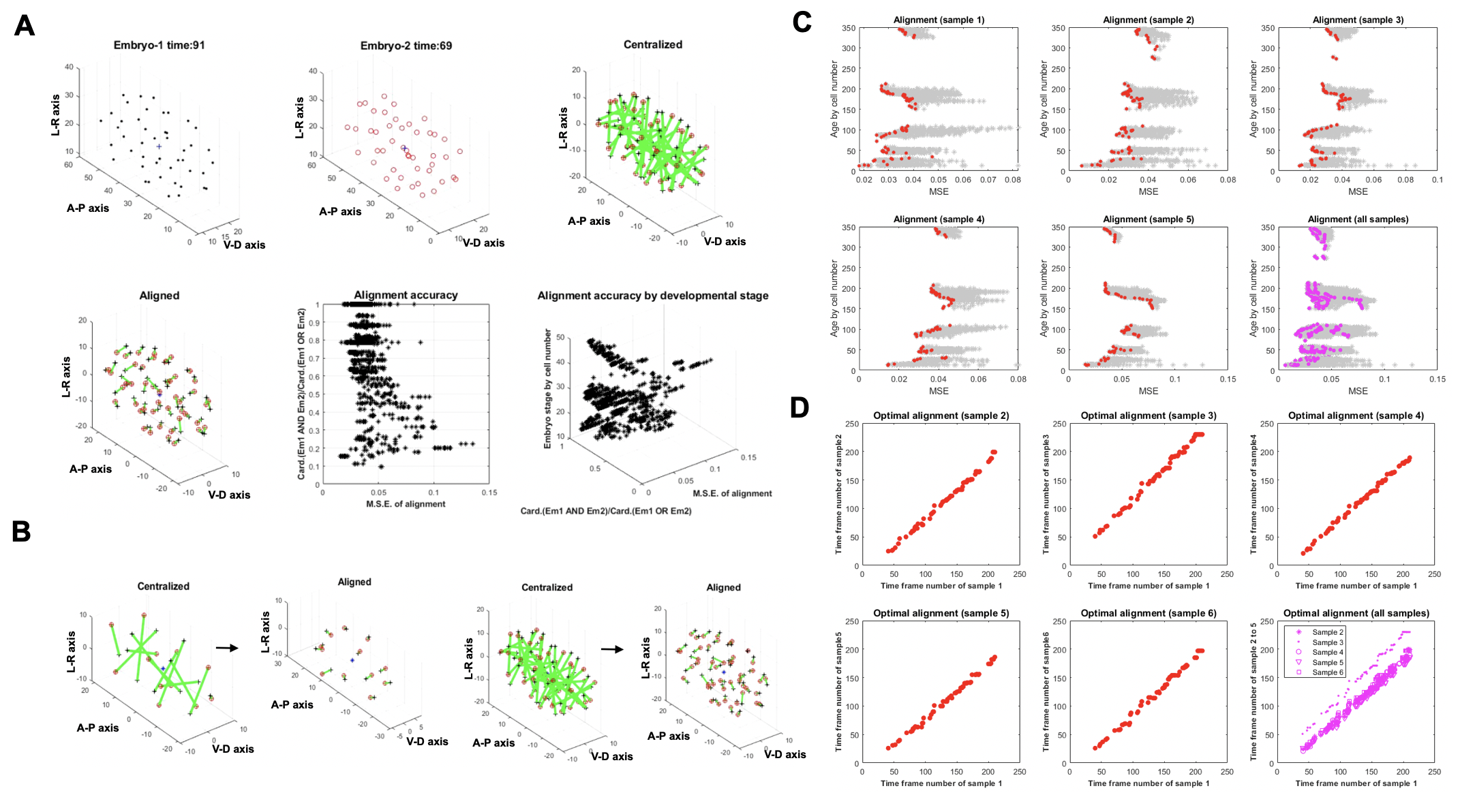
Supplementary Figure 5: Developmental stage specific virtual reference embryo was generated through the alignments of cell positions across all embryo samples. (A) The cell nuclear positions of the control embryo sample (shown as black solid circles) in the EPIC database were utilized as the template for 4-dimensional graphics registration. All the other embryo samples (cell coordinates shown as red open circles) were aligned to this template model. For each pair-wise alignment, the cell coordinates of the two embryo samples were first centralized. The Mean Squared Error (MSE: green bars) that indicated the spatial discrepancy between the two embryos before alignment was calculated with the corresponding cell types (black and red cross). The Pruscrustes algorithm was applied to identify the optimal scaling, rotation and translation mathematical transforms that minimize MSE. In addition to MSE, we also calculate the ratio of the number of common cell types over the number of all the cell types in the two embryos. The higher the ratio number is, the more similar the two embryo samples are in terms of cell population identity. We made use of both the MSE and the ratio number as the optimal criterion for conducting 4-dimenional alignments. (B) Alignments were performed with the template model for each developmental stage. (C) The alignment procedure was applied to all the samples in the database. Five representative sample alignments were illustrated for example. At each developmental stage, the optimal solution of alignment has the minimal MSE value and the largest cardinality ratio number. The red and the gray dots represent the optimal and the sub-optimal solutions identified respectively. (D) The optimal alignment procedure synchronizes the development time of embryos in silico, as indicated by the scatter plot, where X- and Y-axis represents the matched video recording time frame number identified in the pairs of samples.